Quantifying Piece Activity

In the past, I already experimented with a primitive version of calculating the piece activity, which worked by adding up the number of squares a piece attacks, with some bonuses if the square is in the opponent’s half or around the opponent’s king.

This first version worked reasonably well, but there were also issues I wanted to fix. The biggest being that long range pieces would usually be more active than short range pieces, as they attack more squares. This made comparisons between them impossible.

Another thing that bugged me was that even the most inactive pieces are attacking squares. So exchanges necessarily lead to a decrease in the total activity, which made comparisons of different game phases difficult.

So now I’ll make a second, more sophisticated attempt at finding a way to quantify piece activity in a given position, with the hope that this approach will better transfer across different types of positions and make the activity of individual pieces comparable.

Activity of individual pieces

The logical place to start with the activity of a position is to define an activity value for an individual piece.

I decided again on an approach based on the squares a piece can move to (note that this doesn’t include attacked squares that are occupied by friendly pieces). This time, I took a more granular approach to ranking the squares and I came up with the following values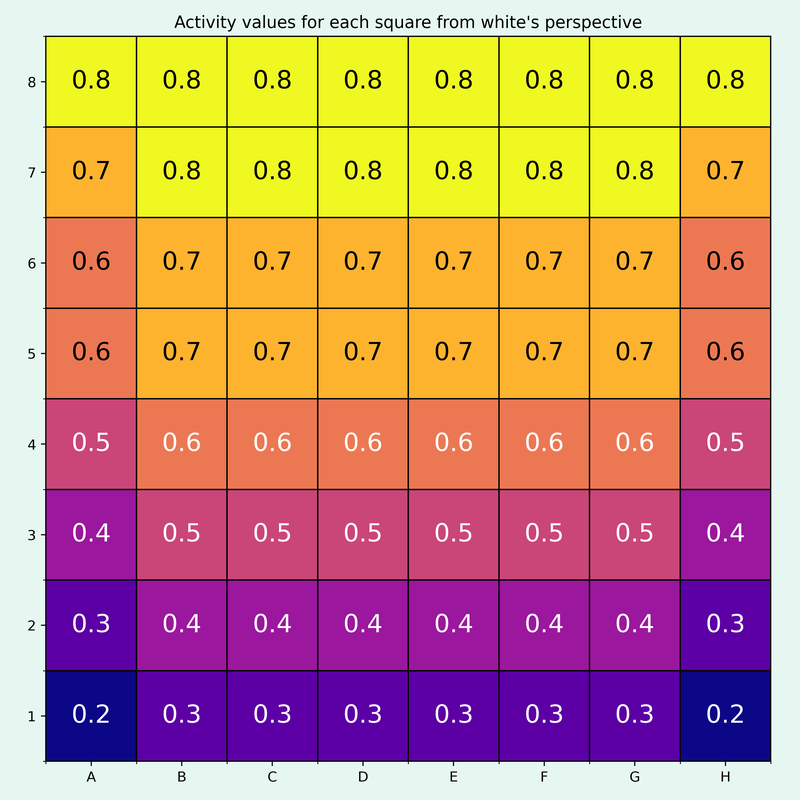

Since squares around the opponent’s king are crucial to control, I also added bonuses to the value of these squares. I decided to give a bonus of 0.2 for the squares behind the king, 0.5 for the king square itself and 0.3 for all other squares the king can move to. Note that I capped the maximum for each square at 1.
These values are of course not perfect, but I looked at many different positions and felt that the results were quite decent.

To get from these values for individual squares to the activity of a piece, I first needed to think about ways to make the activity of different piece types comparable.

Balancing different piece types

My main concern was the balance between short range (knights and kings) and long range (bishops, rooks and queens) pieces.

My main problem was that long range pieces almost always cover useless squares in their own half, whereas a knight on the sixth rank only covers squares from the fourth rank and up. This would mean that the average of long range pieces would get dragged down by the useless squares they cover, even if they also cover very important squares.

I implemented two things in an attempt to reduce the advantage that short range pieces get from averaging the activity values of the squares they can move to.
First of all, I decided that knights and kings should always be assumed to have at least 6 moves. If they have fewer than 6 moves, their score will be negatively impacted (zeros will be added to the calculation of the mean).

Secondly, I didn’t calculate a normal average for the values, but used a generalised mean to give more weight to the important squares. I used the following formula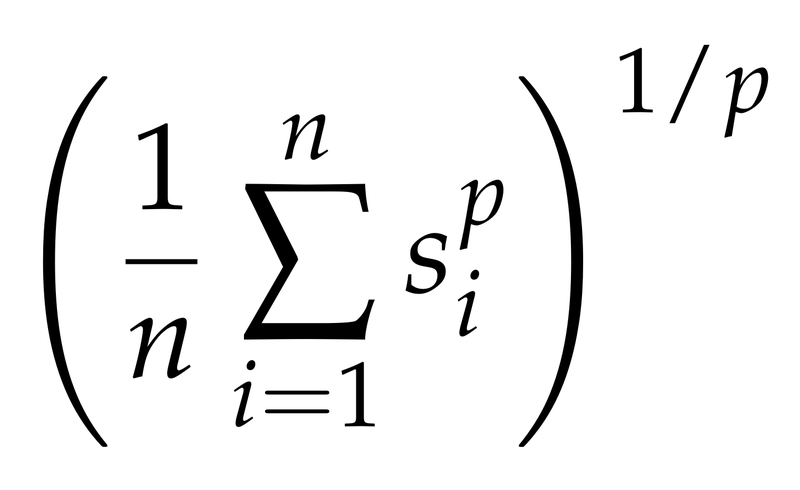

where a piece is attacking n squares and the s_i are the values of the different squares. By using a value above 1 for p in the formula, more emphasis will be put on the more active squares. I chose a value of p=2 but this could be tweaked.

Activity of positions

To calculate the activity of a position, I again take the generalised mean of the activity of the individual pieces. As with the activity for the sliding pieces, I wanted to find a balance between a single non-active piece not reducing the activity of the position too much while still rewarding positions without any inactive pieces.
I also added the ability to exclude the king from the activity calculation and I usually did that for middle game positions.

To get a feeling of the score, here is an example from a game between AlphaZero and Stockfish:

In this position, black has an active rook on a3 and the bishop on a5 also has a high activity score, mainly because it attacks d2 and e1. These two pieces are the main reason why Black has overall a higher score with 0.56 compared to White’s 0.53.
In the game, AlphaZero proceeded with trading off Black’s active rook and the potentially active light squared bishop to reach the following position:

This increased the activity of White’s position to 0.56 while it reduced the activity of Black’s position to 0.52.
You can find the activity of each piece and a couple more examples in this Lichess study.

As I mentioned before, one issue I wanted to fix with this new score is that the activity stays more stable after exchanges.
To see how the score changes over the course of a game, I used the famous game Steinitz-von Bardeleben, 1895 as an example. In this game, 3 pairs of minor pieces were exchanged from moves 11 to 13, which makes it interesting to look at.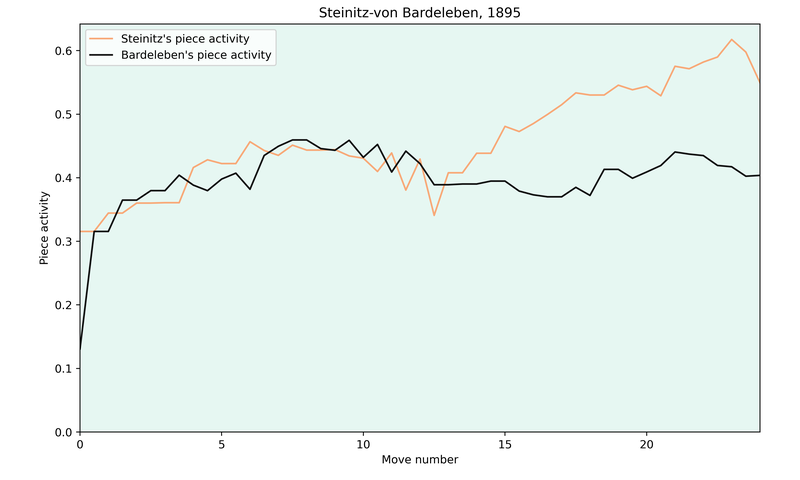

The activity for white fluctuates as the exchanges occur, but I think the main reason is that Steinitz exchanges his active pieces and then uses the next move to activate one of his remaining pieces. Overall, the activity on move 10 before the exchanges is similar to the activity on move 14, after the pieces were exchanged.
It’s also good to see that white’s activity is steadily increasing after the exchanges, which is also my feeling when going over the game.

Limitations

As mentioned before, the individual values probably need some tweaking, but there are also some bigger limitations to my approach that I want to point out.
First of all, I’m still not completely happy with how the averaging works for sliding pieces. One big issue is that having fewer legal moves may be an advantage for the activity.
For example, if white has a bishop on b2 and a rook on a1, the bishop can’t move to a1 and so the square won’t be counted towards the activity. However, if the rook moves away from a1, the bishop can move to this square and as the value of a1 is very low, the activity of the bishop will decrease, even though it has an additional move.
I thought about different ways to prevent this issue, like using a fixed number of squares that count for the average, like I did for knights and kings. However, I didn’t go for this, as there are many cases where a sliding piece can cover a lot of important squares, which will be ignored if the fixed number of squares is too low.

Another problem is based on the fact that pieces are often attacking protected squares. Take the following example from a game between LC0 and ScorpioNN:

It’s clear that the black bishop on b8 can’t move anywhere, but it’s still considered more active than both rooks and its activity is actually close to the activity of the black queen. I don’t want to completely ignore the squares the bishop attacks, as covering d6 in particular can be very useful. However, reducing the value of squares that are attacked by lower valued pieces of the opponent may be an idea.

Closing thoughts

I’ll try to make an interactive version of this score, so you can play around with the values yourself and test different positions. This should hopefully be done in a couple of weeks.

Another important thing to mention is that I only counted pieces that are active in an attacking sense. There are certainly situations where a piece is very important in defending important squares, but I didn’t count that for this post.

While finishing this post, I also thought about somehow combining this piece activity with the square control I wrote about a couple of months back. If pieces are all “over attacking” the same squares, the position as a whole may not be as active as it appears when looking at the pieces individually. But I couldn’t think of an easy way to combine these two things and I didn’t want to make it too complicated.

Let me know what you think about this new activity score and if there are any big things you’d want to change.

---

If you enjoyed this post, check out my Substack.